A
biologia moderna está, em grande parte, baseada nos conceitos
da físico-química e em especial da teoria cinética,
pela qual é conceituado que todas as partículas
de dimensões atômicas e moleculares estão
em constante movimento, em todas as temperaturas acima do zero
absoluto (-273,16 oC). Por meio da suposição de
que as moléculas se movem constantemente é possível
explicar processos como a difusão, reações
químicas, pressão dos gases, potencial hídrico,
e diversos outros fenômenos ocorridos nas plantas. Uma visão
geral sobre os conceitos de energia livre será de grande
valia no entendimento dos princípios termodinâmicos
envolvidos nesta discussão.
2.1 Relações
energéticas do sistema água-planta
A complexidade do sistema água-planta requer o emprego
dos conceitos da termodinâmica para definir as interações
físicas ocorridas e expressar o "status" energético
da água. A energia associada ao sistema água-planta
é de natureza cinética e potencial. A contribuição
do componente cinético é relativamente baixa devido
à baixa velocidade do movimento da água nas plantas.
Entretanto, a água neste sistema possui energia potencial
desde que se desloca em resposta a certas forças inerentes
ao organismo vegetal.
A água nas células e por extensão nos tecidos
busca constantemente o equilíbrio termodinâmico
obedecendo à tendência universal de se mover dos
locais onde apresenta maior energia para aqueles, onde o nível
energético é mais baixo. Isto confere um caráter
dinâmico, ou seja, que varia temporalmente e espacialmente.
Estas relações ficarão mais claras quando
da discussão dos conceitos de potencial hídrico
e de seus componentes.
2.1.1
Conceitos de energia livre
As plantas e os animais necessitam de um contínuo suprimento
de energia livre, sem a qual, eles entrariam em equilíbrio,
e como conseqüência cessaria a vida. O sol é
a fonte primordial de energia livre e por meio da fotossíntese
as plantas armazenam a energia radiante sob a forma de compostos
intermediários ricos em energia, como ATP e NADPH+H+
, e posteriormente sob a forma de ligações químicas
que resultam quando o CO2 e a água reagem para formar
os carboidratos. Na respiração, a energia livre
é reconvertida a ATP, sendo utilizada para realizar trabalho
biológico.
Ao invés de estudar todo o universo a termodinâmica
define pequenas partes do mesmo, que são chamadas de
sistemas . Um sistema pode ser uma célula, uma folha
ou mesmo toda a planta. Quando um sistema passa de um estado
A para um estado B, a quantidade mínima de trabalho necessária
para ocasionar esta mudança pode ser definida como o
aumento da energia livre associado com esta alteração.
Por outro lado, o decréscimo da energia livre quando
o sistema passa do estado B para o estado A, representa a quantidade
máxima de trabalho que pode resultar desta transição.
Assim, os limites de trabalho feito no sistema ou pelo sistema
quando ele passa de um estado para o outro, estão relacionados
a mudanças de energia livre. Por exemplo, na Figura 3,
o sistema admitido é o universo em dois instantes, momento
atual e pré-big bang.
O conhecimento da energia livre sob uma condição
quando comparada com a existente em outra, nos permite predizer
a direção de uma mudança espontânea.
Em um sistema sob condições de temperatura e pressão
constantes, numa mudança espontânea sempre se verifica
o decréscimo de energia livre.
A maior parte dos sistemas biológicos está submetida
às condições de temperatura e pressão
atmosférica constantes, pelo menos por curtos períodos
de tempo. Para estas condições, a energia livre
de Gibbs representa a capacidade de um sistema realizar trabalho,
sendo determinada pela contribuição aditiva de
cada espécie que compõe o sistema.
A energia livre de Gibbs está relacionada com a energia
total do sistema pela fórmula que expressa a 2a lei da
termodinâmica .
Equação
1
Onde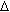 
G
expressa a variação da energia livre de Gibbs,
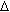H a variação
da energia total do sistema e T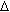S
a energia não disponível para realizar trabalho,
sendo T a temperatura do sistema (oK) e S a entropia. A entropia
é um parâmetro termodinâmico que mede o estado
de desorganização do sistema que está intimamente
correlacionado com o equilíbrio que é atingido
quando a entropia atinge um ponto máximo.
Figura 3. Esquema mostrando dois momentos distintos do universo.
Em B, o momento pré-big bang é representado, note
que o grau de desordem é mínimo e o conteúdo
de interno de calor do universo pode ser considerado máximo,
neste instante, a matéria estava concentrada em um mesmo
ponto. Enquanto em A, a partir do big bang, a entropia (desorganização)
do universo tende sempre à elevação e o
conteúdo interno de calor do sistema tende ao declínio.
Note que se a mudança fosse de A para B, seta inferior,
haveria a necessidade de entrada de energia para que o processo
ocorresse.
2.2 Potencial hídrico
Fluxo em massa ocorre em resposta a um gradiente de pressão,
envolvendo um grupo de moléculas que se movimentam juntas
(água + solutos).
Quando a diferença de pressão é estabelecida
pela gravidade (por exemplo, peso do fluído), tem-se
a pressão hidrostática. O fluxo em massa nos tecidos
vasculares pode ocorrer devido a diferenças de pressão
criadas pela difusão.
Normalmente, a água e os solutos entram e saem das células
vivas não por fluxo em massa, mas uma partícula
(molécula) de cada vez.
"Chama-se difusão ao movimento espontâneo,
ao acaso, de partículas individuais (moléculas
ou íons), devido à sua energia cinética".
Todas as moléculas estão em constante movimento
acima do 0º absoluto (0º Kelvin = -273ºC) e possuem
certa quantidade de energia cinética. Geralmente não
se observa claramente a difusão, pois é muito
lenta quando se trata de distâncias macroscópicas,
e o fluxo em massa de líquidos e gases é muito
comum. Observa-se difusão ao colocar cristais de açúcar
ou corante em água; as moléculas do soluto se
difundem para as regiões menos concentradas, e as moléculas
de água se difundem, ao mesmo tempo, das regiões
mais concentradas em água para onde estão os cristais
(Figura 4). O equilíbrio se estabelece quando as moléculas
de água e soluto estiverem distribuídas igualmente.
A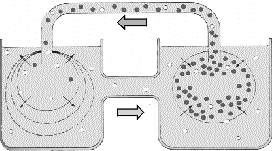
B
Figura 4. Esquema mostrando dois sacos revertidos por uma membrana
semipermeável (por exemplo, celofane) imersos em um recipiente
contendo água, interligados por um tubo. No saco B foi
adicionado um soluto (e.g. açúcar). Deste modo,
as moléculas do soluto (pontos escuros) se difundem para
as regiões menos concentradas, em direção
ao saco A, e as moléculas de água (pontos claros)
se difundem, ao mesmo tempo, das regiões mais concentradas
em água para onde estão os cristais, em direção
ao saco B.
A Lei de
Fick indica que a difusão pode sempre ocorrer espontaneamente,
a favor de um gradiente de concentração ou potencial
hídrico, até que o equilíbrio seja adquirido.
No equilíbrio, nenhum movimento do soluto pode ocorrer
sem a aplicação de uma forca direcionadora. Na
Figura 4, a forca direcionadora para a difusão da sacarose
é a energia do gradiente, estabelecido no inicio do experimento
por causa da diferença de concentração.
O movimento ou transporte em um sistema biológico também
pode ser direcionado por outras forcas (pressão hidrostática,
gravidade e campos elétricos). Entretanto, em sistemas
biológicos a gravidade raramente contribui substancialmente
como forca direcionadora. Quando o gradiente de concentração
é a fonte de energia potencial esta é definida
de potencial químico de qualquer soluto de acordo com
a seguinte relação:
Equação
2
Na Equação
2, 
j é
o potencial químico da espécie de soluto j em
joules por mol; mjo potencial químico de j em condições
padrão; R é a constante universal de gases; T
é a temperatura absoluta, e Cj é a concentração
(mais precisamente a atividade) de j. O termo elétrico,
zjFE, aplicá-se somente para íons dissolvidos,
z e a carga eletrostática do íon, F é a
constante de Faraday (equivale à carga elétrica
de um mol de prótons), e E é o potencial elétrico
total da solução (em relação ao
padrão). O termo final, VjP, expressa a contribuição
do volume (V) e pressão (P) de j para o potencial químico
de j. Este último termo tem a menor contribuição
para o mj do que os termos de concentração e elétrico.
Desde que a água e uma neutra, e o componente elétrico
não influencia em seu potencial químico.
Assim, utilizando a Equação 2.1 e eliminando os
componentes não significativos para a espécie
água (w) temos.
Equação
2.1
Assim sendo,
o potencial químico da água se resume na seguinte
Equação:
Equação
3
Onde Cw representa a atividade de água, que é
a relação entre a pressão de vapor da água
no sistema (e) e a pressão de vapor da água no
estado padrão (eo).
Em fisiologia vegetal e nas ciências do solo, o movimento
da água, incluindo a difusão, são estudados
em termos de pressão, sendo utilizada a seguinte definição
de potencial hídrico. O potencial hídrico (
w)
é o potencial químico em um sistema ou parte do
sistema, expresso em unidades de pressão e comparado
com o potencial químico (também expresso em unidades
de pressão) da água pura nas mesmas condições
de temperatura, pressão e altura, com o potencial hídrico
da água de referencia considerado como zero. Esta definição
e expressa pela seguinte relação:
w =(
- wo) / Vw
Equação 4
Desta forma,
deve-se dividir os termos de Equação por uma unidade
de volume (Vw) para obter uma unidade de pressão (w).
Deste modo, a transformação de unidade de energia
para a unidade de pressão se processa da seguinte forma:
w
= ( - wo)/Vw
= (RTln (e / eo))/ Vw Equação 4.1
Analisando
a Equação 4.1, pode-se perceber que o potencial
hídrico (w)
é equivalente à diferença, em energia livre
por unidade de volume molal, entre a água do sistema
e a água pura, na mesma temperatura. Se considerarmos
a água pura, o resultado será zero. Normalmente,
a pressão de vapor da água no sistema (e) e menor
do que a pressão de vapor da água no estado padrão
(eo) que assume valor zero, ou seja, normalmente o mw terá
um valor negativo.
No caso da água pura, e = eo e w
= 0. Portanto, o potencial hídrico é, freqüentemente,
negativo nas células; tecidos e solução
e no máximo assume o valor zero para a água pura.
As unidades de R,T e Vw no sistema internacional são
J mol-1 K-1, k-1 e m3 mol-1, respectivamente.
Assim w
= J mol-1 K-1 K / m3 mol-1 = J m-3
w = J m-3
= Pa (Pascal)
As unidades mais freqüentemente usadas são o bar,
atmosfera, e de acordo com o sistema internacional, o pascal
e o megapascal (MPa).
1 bar = O,987 atm e 1 MPa = 10 bar ou 1bar =0, 1 MPa.
Os diversos fatores que afetam o potencial químico da
água no sistema são agrupados e avaliados isoladamente,
constituindo-se nos chamados componentes do potencial hídrico
que são quatro, a saber: Potenciais gravitacional (g),
mátrico (m),
osmótico (s)
e de pressão (p),
ver Equação 4.2.
w = (
- wo)/Vw
= g + m
+ s + p
2.2.1
Componentes do potencial hídrico
O potencial hídrico em qualquer sistema é afetado
por diversos fatores que modificam o potencial químico
das moléculas de água e, por conseguinte, da energia
livre de Gibbs. Para facilitar o isolamento e a avaliação
dos fatores foram caracterizados e definidos diversos componentes
do potencial hídrico.
O potencial hídrico (w)
de um sistema é reduzido pela adição de
substâncias polares e, ou íons ao meio, pois as
moléculas dipolares da água são atraídas
e retidas por estes solutos, induzindo um decréscimo
na atividade da água (cw, na Equação 3).
O potencial osmótico (s)
é o componente que define estas interações
tendo, conseqüentemente, um valor negativo. O p
varia muito pouco na maioria das células vegetais, com
exceção das do mesófilo, floema e estômatos.
A modificação da pressão sofrida pela água
no sistema pode também causar variação
do potencial hídrico. O potencial ou pressão de
turgescência (p)
define estas modificações e resulta da entrada
de água seguindo um gradiente de potencial hídrico
favorável. À medida que a água penetra
na célula, passa a exercer uma força por unidade
de área (pressão) causando uma distensão
na parede, que é contrabalançada por uma pressão
igual mais de sentido contrario, chamada de pressão de
parede. À medida que a parede se distende, sua resistência
às extensões subseqüentes aumenta, de tal
maneira que o desenvolvimento do p
não está linearmente relacionado com mudanças
de volume celular (Figura 5).
O P pode
ser positivo como, por exemplo, em células túrgidas;
podendo também alcançar valores negativos, o que
ocorre nas células do xilema das plantas sob condições
de transpiração intensa ou pode ser igual a zero,
como nas células em estado de plasmólise incipiente.
A ocorrência do p
negativo em outras células que não nos elementos
de vaso do xilema não foi ainda demonstrada experimentalmente.
O potencial mátrico (m),
que também tem um valor negativo, é o componente
do potencial hídrico que define as influências
que as forças de superfície dos colóides
e espaços intermicelares exercem sobre o potencial hídrico
da água. Embora estas interações pudessem
ser adequadamente representadas pelas suas contribuições
aos potenciais osmóticos e de turgescência, o potencial
mátrico permite o isolamento e identificação
destas forças de uma maneira mais específica.
O conceito de potencial mátrico é extremamente
importante na caracterização do processo de embebição
e estudo das relações hídricas no solo
como discutiremos posteriormente.
O potencial gravitacional (g)
expressa a ação do campo gravitacional sobre a
energia da água. Ele é definido como o trabalho
necessário para manter a água suspensa em determinado
ponto em relação à atração
da gravidade. O potencial gravitacional também não
é medido como um valor absoluto e para determinar sua
magnitude é necessário atribuir um ponto de referência
arbitrário, no qual o g
é igual a zero. Normalmente, a superfície do solo
é tomada como referencial.
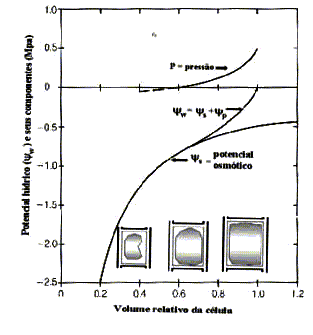
Figura 5.
Diagrama de Höfler, Os componentes do potencial hídrico
(w) sofrem
mudanças à medida que a célula fica túrgida.
O potencial osmótico (s)
é calculado levando em consideração a alteração
do volume celular, ou seja, segundo uma curva de diluição,
ver Equação 5. A curva de pressão (P) é
arbitrária, mas expressa o fato de que as células
com pressão zero podem absorver água. Inicialmente
o incremento da pressão dentro da célula é
lento, em seguida se torna rápido. Aumentando o volume
da célula o potencial osmótico, torna-se mais
positivo. A curva de potencial hídrico é a soma
algébrica das curvas de pressão e potencial osmótico.
De acordo com a seguinte Equação, a saber: =
P - s.
O g
em um dado ponto na planta situado a um metro acima do solo
(referencial) apresentará um g
de cerca de +0,01 MPa. Este componente de potencial hídrico
se torna importante somente quando do estudo do movimento de
ascensão da água nas plantas de grande porte e
percolação da água através dos poros
do solo.
Portanto, para uma célula vegetal, sob condições
isotérmicas, a Equação abaixo expressa
a ação de todos os fatores acima descritos sobre
o potencial hídrico de uma célula vegetal.
Componentes do potencial hídrico
w = g
+ m + s
+ p